There are as many different concert pitches as there are notes on a piano. Well… almost. What do I mean by that? Although there are other concert pitch articles on this site, I’ll quickly give you the low down. Setting the concert pitch requires tuning all notes to one specific note. Right now, the international standard concert pitch is A=440, although some countries use A=442 or A=444.
NEWS FLASH! It has been wrongly stated in internet land that the standard concert pitch before the 1940’s was set at A=432. That is simply not true and there’s plenty of musical and historical evidence to prove it. Talk to any piano tuner if you still question my statement.
Image by Pixabay
When I say “Pythagorean” tuning (temperament), that refers to the distance between all the notes in a scale. A concert pitch can’t be set until a temperament is chosen. There weren’t issues with temperament until composers started writing in a variety of keys. Basically, once people, such as Johann Sebastian Bach, decided to add all those sharps and flats, we had problems. It was a race from that point on to find the best form of tuning instruments so that all keys sounded in tune. Up to that point, there were long intermissions between pieces of music so the keyboards (usually a harpsichord or pianoforte) could be re-tuned to play in a different key. Coffee break, anyone?
Before the age of the keyboard, tuning was simple. Most musicians stuck with Pythagorean tuning or Just intonation. The concert pitch was often set by the town church bell (so I hear). If you look at Renaissance music, key signatures are simple. Rarely was music written with more than two sharps or flats. Straying away into foreign keys (i.e. lots of sharps and flats), wreaked tonal havoc. Therefore, musicians could play in a few simple keys without having to re-tune between musical selections.
If you’re not musically inclined, you’re probably thinking, “what the heck!?” Well, the tuning problems lie with the distance between notes. Major thirds (C – E for example) are generally too wide (sharp). Perfect fifths (C – G) and Perfect fourths (C – F) and Perfect octaves (middle C to the octave higher) all are very close, no matter what temperament is used. That’s why they’re called “perfect” intervals. Thirds, sevenths, and seconds – watch out! The distance between C – E and G – B (both Major thirds) vary in every temperament other than equal temperament (our modern standard). Basically, instant small adjustments have to be made, especially when more than one instrument play together. Singers automatically make adjustments by ear. Playing or singing “in tune” requires getting rid of the “beating” between two notes so the pitches lock in. When two intervals match perfectly, the tones are much richer because they are truly in tune.
Equal temperament is equal mathematically but it’s not equal tonally. We’ve become used to it because it’s close… but not quite perfectly in tune. Keyboard and fretted instruments are not able to make adjustments on the fly. Their instruments are “fixed” tuning, meaning that they don’t have the ability to adjust while performing. Outside of keyboard and fretted instrumentalists, I can safely say that most good musicians do NOT stick to equal temperament. We learn to “lock into” the chord and/or tonal structure of the music by making small adjustments when needed. Wind players do it with alternate fingerings, change in voicing, or sometimes embouchure (mouth position). String players move fingers up/down slightly on the string.
What does this have to do with Pythagorean tuning? First of all, it’s important to understand that Pythagorean tuning is actually Pythagorean temperament. The distance between notes in the Pythagorean scale are not equal. As musicians perform using the Pythagorean tuning, they still have to make adjustments, by ear. To the untrained ear, it’s difficult to hear the difference between a Pythagorean scale and an equal tempered scale. Go to YouTube and listen to people play the two scales. There are several videos to choose from.
No matter what temperament or concert pitch is used, musicians still have to pay attention to tonal structure. As a clarinetist, when I’m holding a G for several beats and it’s the Perfect fifth of the chord, I tune that fifth so it locks in. But, the moment the chord changes and that same G becomes the Major third, I have to literally lower it quite a bit before it locks back into the tonal structure of the new chord. By nature, Major thirds are going to be sharp. This is one reason it took so long for musicians to start using it. At one time, the Major third was considered a dissonant interval. Pythagorean Major thirds are sharp so, performers had to adjust. With the instruments of that time, it was tough to do. The best musicians learn to understand chord structure and how every note should fit within any chord. In addition, every instrument will have tuning issues specific to that instrument. Yes, my friends, it takes years of practice to learn how to play in tune with other musicians.
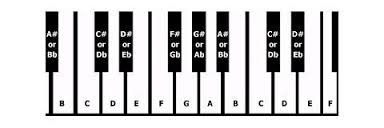
Moving right along – since I’m fond of the A=432 concert pitch, I put all the pitches for the A=432 concert pitch using Pythagorean ratios (AKA – Pythagorean temperament). I’ve calculated them according to a video I watched by Aloixa Sinclaire. CLICK HERE for that video. She completed the first octave, managing to get rid of the Pythagorean comma, and I did the rest from there. The ratios she used: 9:8 (Major second or whole step) and 256:243 (minor second or half step). For example: C to D is a Major second (whole step) and C to C# is a half step (minor second). Sinclaire explains how to resolve the Pythagorean comma issue using these ratios. Here’s a keyboard as a visual for you…
The only problem with any chart like this? It’s great until you actually start using it because a good musician will still make adjustments. Therefore, pitches will not be exactly what’s listed below. Why? It depends on the intervals/chords in the music. Remember that music from the time of Pythagoras until about the 1400’s was very simple. Our music is much more complex so using these exact frequencies for any piece of music would be impossible. These frequencies are a starting point only. There will be minor adjustments depending on the instrument, the structure of the melody, and the accompaniment. The point I’m making is that unless a musician is completely clueless to any form of tuning, they’re going to make adjustments as needed and won’t stick strictly to any temperament.
It’s possible to choose a main frequency. Let’s say you really want to focus on 729 Hz (an F# in the A=432 concert pitch)… you’d use that note to set the concert pitch. Then, tune all other notes to that F#. But, understand that any other notes played will be very close by not quite to the other frequencies on this chart if you’re using Pythagorean tuning.
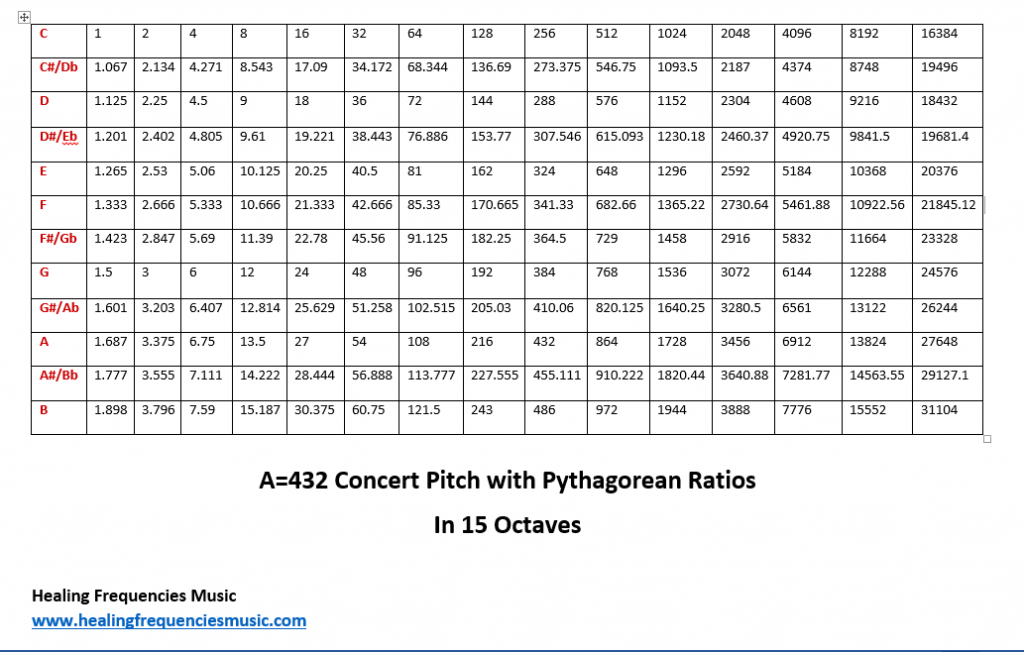
You’ll see how everything starts with the number 1. As noted in many other places on this site, the A=432 concert pitch fits nicely to things found in nature. You should recognize some of those numbers from this chart. You’ll also notice that the higher the frequency, the larger the distance between numbers. So, if you’re looking at 729 Hz (F#), in other charts, they show this same note as being 720 Hz. They are close enough at that high frequency range, it would be difficult to tell the difference. At the lower frequencies, even a .01 change in frequency will make a difference. So, keep that in mind when you’re comparing this to other frequency charts.
Now, for some fun, I re-figured this chart using A=444 as the concert pitch in Pythagorean temperament. You’ll notice that on many sites and charts, they list the C above middle C as being 528 Hz. However, in this chart, it’s listed as 526.222 Hz. Again, this is Pythagorean tuning based on the Pythagorean seconds. It’s so close to 528! As an example, my clarinet is tuned to A=440. But, if I put on a short barrel (the piece just below the mouthpiece) and make some other adjustments, I can actually play that C at 528 Hz even though my instrument is made to play it at 523 Hz. It’s all about learning to adjust as needed. And, A=444 is close enough to A=440 that most modern instruments should have the ability to play in A=444.
NEWS FLASH! I hate to say it but most ensembles play sharp anyway even though they tune to A=440. The final pitch tends to hover around A=442! When I went to a competition in France, I was told in advance that they tuned the pianos to A=442. For the first time in my life, I didn’t have major tuning issues to a piano! Eventually, I purchased a longer barrel so playing with pianos tuned to A=440 wasn’t such a big deal. Either way, I know pianos are in equal temperament. And, I have to learn to make necessary changes so I don’t sound out of tune when playing with a piano. Anyone who collaborates with a piano struggles because it can’t change pitches mid-performance. Playing with an orchestra or band is a whole different animal! I won’t go into that here.
With that, here’s the same Pythagorean ratio tuning chart for the A=444 concert pitch…
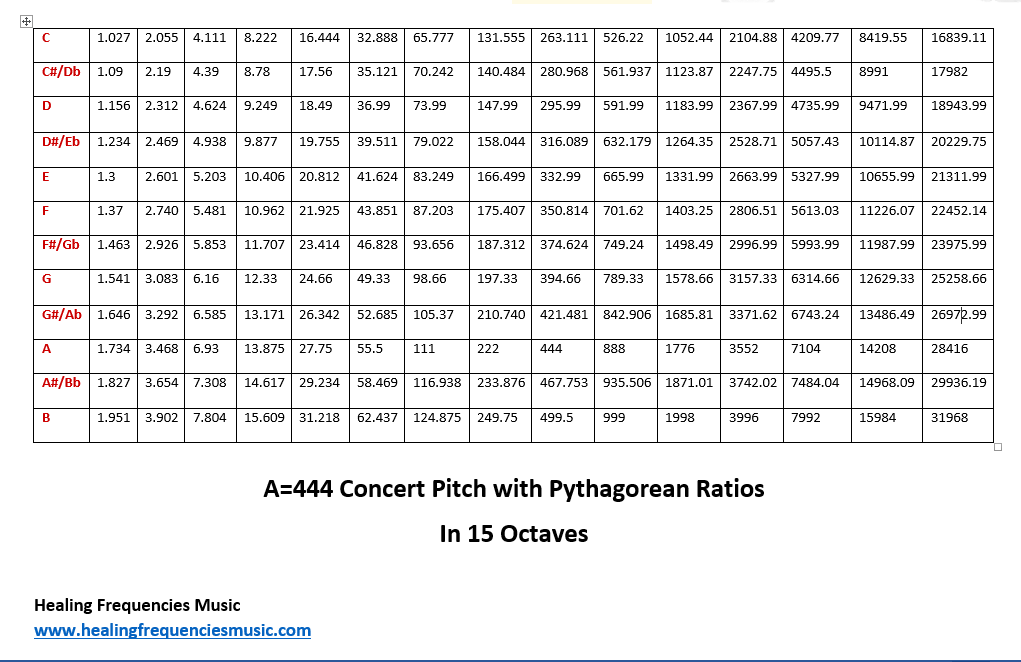
Feel free to use these charts for your own research! If you’re interested in some of my instrumental music in A=444, try the “528 Creative DNA” album. One of the customer favorites for the A=432 concert pitch is the album “I AM.” To hear samples of all my music, check out the Samples page.
Happy hunting and don’t forget to send me cool articles on all things frequency related!
Del
© 2018 by Del Hungerford
[mailerlite_form form_id=2]